eFatigue gives you everything you need to perform state-of-the-art fatigue analysis over the web. Click here to learn more about eFatigue.

BS 7608 Welds Technical Background

Welds may be analyzed with any fatigue method, stress-life, strain-life or crack growth. Use of these methods is difficult because of the inherent uncertainties in a welded joint. For example, what is the local stress concentration factor for a weld where the local weld toe radius is not known? Similarly, what are the material properties of the heat affected zone where the crack will eventually nucleate. One way to overcome these limitations is to test welded joints rather than traditional material specimens and use this information for the safe design of a welded structure.

One of the most comprehensive sources for designing welded structures is the Brittish Standard Fatigue Design and Assessment of Steel Structures BS7608 : 1993. It provides standard SN curves for welds.

For purposes of evaluating fatigue, weld joints are divided into several classes. The classification of a weld joint depends on:

• the macroscopic geometry of the pieces welded,
• the direction of the cyclic stresses, and
• the location of the crack that leads to failure.

Two fillet welds are shown below. One is loaded parallel to the weld toe ( Class D ) and the other loaded perpendicular to the weld toe ( Class F2 ).

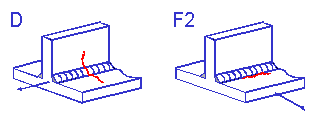
It is then assumed that any complex weld geometry can be described by one of the standard classifications.

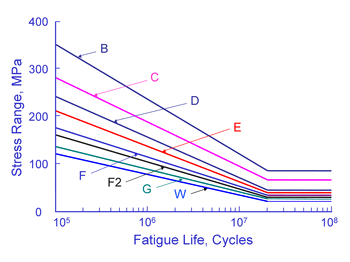
The curves shown above are valid for structural steel welds. Fatigue lives are not dependant on either the material or the applied mean stress. Welds are known to contain small cracks from the welding process. As a result, the majority of the fatigue life is spent in growing these small cracks. Fatigue lives are not dependant on material because all structural steels have about the same crack growth rate. The crack growth rate in aluminum is about ten times faster than steel and aluminum welds have much lower fatigue resistance. Welding produces residual stresses at or near the yield strength of the material. The as welded condition results in the worst possible residual or mean stress and an external mean stress will not increase the weld toe stresses because of plastic deformation. Fatigue lives are computed from a simple power function.

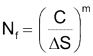
The constant C is the intercept at 1 cycle and is tabulated in the standard. This constant is much larger than the ultimate strength of the material.

The standard is only valid for fatigue lives in excess of 10⁵ cycles and limits the stress to 80% of the yield strength. Experience has shown that the SN curves provide reasonable estimates for higher stress levels and shorter lives. In eFatigue, the maximum stress range permitted is limited by the ultimate strength of the material for all weld classes.

Test data for welded members has considerable scatter as shown below for butt and fillet welds.

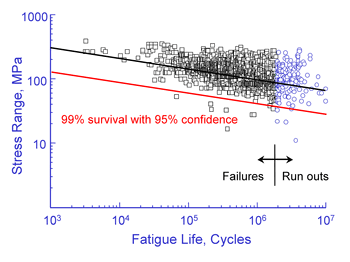
Some of this scatter is reduced with the classification system that accounts for differences between the various joint details. The standard give the standard deviation of the various weld classification SN curves.

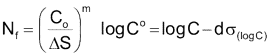
The design criteria d is used to determine the probability of failure and is the number of standard deviations away from the mean. For example d = 2 corresponds to a 2.3% probability of failure and d = 3 corresponds to a probability of failure of 0.14%.